La tecnología es inmanente a los humanos. Si se requiere saber hasta dónde se desarrolló una sociedad, el juicio será otorgado observando la tecnología elaborada por dicha sociedad. La tecnología es entonces una arma de dos filos. Puede ser para empoderar la mente de las personas, mientras que puede enajenar la mente de otras personas. Y cuando se menciona a la innovación: como una mejora del proceso, por ejemplo en el proceso enseñanza aprendizaje:

Lo que se relata a continuación es una estrategia para el aprendizaje de un tema de la Geometría.

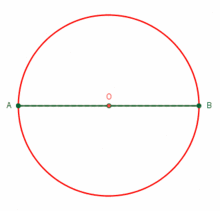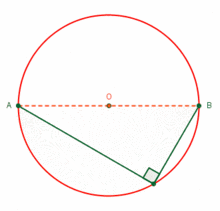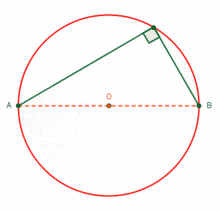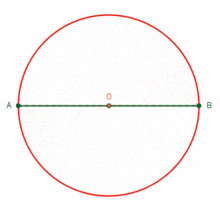
Cuenta la historia que cuando viajaba Tales de Mileto (Mileto, 625/624 a. C.-ibídem, 547/546 a. C), comerciante, matemático, físico y uno de los Siete Sabios de la antigüedad en la cuna de la civilización occidental, hoy en Turquía; por Egipto y otras regiones donde se proveía de las mercancías que llevaba a Mileto. No solo observó formas de desempeño de otras civilizaciones sino que también aprendió. Y así propuso teoremas matemáticos como el del ángulo inscrito. Hoy lo podemos comprender con una simulación en formato .gif Y no mencionarla con notación de las matemáticas que requieren de conocimientos sobre la nomenclatura ¿Cómo podrías, tu lector, dar a conocer este teorema fundamental de la geometría? Observa cómo se mantiene constante el ángulo recto del triángulo rectángulo que se forma conforme se mueve el vértice sobre la circunferencia. (Ver figura 1)

Figura 1

Pues un discípulo de este sabio de la Grecia de la antigüedad fue Pitágoras ( Samos, c. 569-Metaponto, c. 475 a. C.) filósofo y matemático considerado como el primer matemático puro. Hay datos escasos de él, no existen textos de su autoría ni biografías oír sus contemporáneos. Hay demostraciones supuestas de su teorema desarrollados por el mismo Pitágoras. Y una gran cantidad de demostraciones de otros autores. Pero lo que nos mueve a esta estrategia es mencionar que su teorema fue ponerlo en papel con notación matemática, ya que era algo conocido a través de la práctica por los geómetras egipcios, a quienes observó seguramente por sugerencia de su maestro Tales, y en el extremo oriente por los chinos. Todos estas formas del conocimiento para cumplir con el significado de Geometría: medida de la Tierra. (Ver figura 2)

Hoy en la escuela cuando se menciona a la Geometría, en la mente de los que participan en el proceso enseñanza aprendizaje, asocia con esta palabra; escuadras, compás y papel.

Por lo que se sugiere que los estudiantes conciban que el saber no puede aislarse del hacer. El caso de Pitágoras es un ejemplo del trabajo de síntesis que se hace con la matemática sobre los conocimientos adquiridos en la práctica del día a día.

Si ahora se va más allá de las figuras regulares de la geometría de los griegos: triángulos, cuadrados, trapecios, … donde las figuras irregulares no son contempladas, quizás menos lo que ocurre con los trapecios.  ¿Será una “simplificación” para poder dosificar a los alumnos los saberes que deben aprender en la escuela?

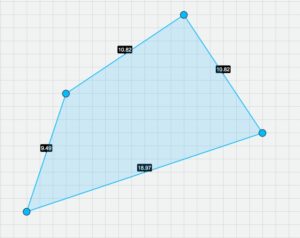
Figura 3

Seguimos con la clase de matemáticas, rumbo a las matemáticas superiores:

Supongamos que tenemos el siguiente terreno y deseamos medir su superficie. El inconveniente es que tiene una forma irregular. (Ver figura 3.) Las veces en la que se presenta este problema a los estudiantes y recurren a triangular el terreno para sumar las áreas de los triángulos formados, se tienen pérdidas de información del 30 al 40%. Ya que no se encuentra el área del terreno con una eficacia del 100%.

Cuando el trabajo de los investigadores de las ciencia duras, como ocurre con la matemática; se tienen avances que denotan creatividad e imaginación. En este caso lo hecho por un matemático vienés Georg Alexander Pick (1859- 1942) utilizando lo que se conoce como un geoplano. (Ver figura 4) Hoy se puede contar con tecnología digital para explorar con el Geoplano, lo cual puede hacerse desde la computadora o la tableta. Visitar la herramienta propuesta en la página de Math Learning.

Y usted docente, puede bajar a su computadora un documento con una secuencia de clases, apoyándose en el geoplano, para encontrar y cuantificar áreas de figuras geométricas de forma irregular, entre ellas la encontrada por Pick, a quien ya se mencionó. Haz clic en >>> GeoplanoSecundariaPick

Figura 4

Este matemático encontró una forma de calcular áreas de forma tal que si se cuentan el número de clavos incluidos y el número de clavos en el perímetro se puede calcular el área precisa de la figura irregular. Se puede utilizar una aplicación, que utiliza el Teorema de Pick, para el cálculo de áreas en www.matetic.org

Un dilema para seguir con el ciclo de aprendizaje

Cuando se tiene que aprender un algoritmo, y hoy que las calculadoras y las aplicaciones nos evitan ejecutar el algoritmo, y nos dan éstas el resultado de manera casi inmediata. ¿Un docente debe enseñar el algoritmo, o tan solo mencionarlo y pasar al uso de la tecnología? ¿Cuáles de estos algoritmos, al usar tecnología, dan un resultado preciso? En este caso para el cálculo del área con el Teorema de Pick, se tiene una certeza del 100%. Y en el caso del cálculo de la raíz cuadrada de un número. ¿En que consiste la certeza del algoritmo empleado por una calculadora “barata” y el de una calculadora “profesional”?

Involucrar a los estudiantes en la forma en la que dan a conocer sus evidencias, hoy con las tecnologías digitales, los llevan aprendizajes significativos y más profundos. Ya que cuando aprenden a decir cómo se hacen las cosas, aprender a redactar y ponerlo de manera que se entienda en los medios conocidos como blogs, wikis o sitios. Ver por ejemplo: plazacomunitariacarrasco.blogspot.com